注意：这是一篇从旧博客恢复的文章。

原地址：http://freemeepo.com/blog/archives/88

---

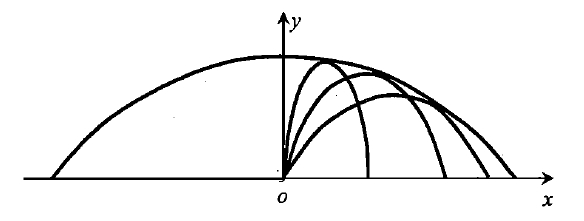
几天前在做ACM组队赛训练的时候，遇到了这么一题（URAL 2008）。读懂题目之后发现其实是从原点抛出一个物体，求达到横坐标x时，纵坐标y可达到的最大高度。

用编程的方法也是可以暴力求解的。不过这其实就是个简单的抛体运动的包络面问题，以前的学过的。但是当时推了半天都推不出来。最后很机智地使用了待定系数法把公式推了出来。具体方法是：肯定90度上抛达到的最高点坐标一定是包络面的顶点，45度抛出达到地面的点一定是包络面上的一个点。另外我知道包络面也是个二次函数（抛物线），于是就可以求得包络面了。

但之前我花了很长时间都没推出来，即使我还隐约记得是让某个方程的$$\Delta=0$$就可以了。

赛后查了资料，终于知道怎么推的了。现记录如下：

首先建系，写出方程$$!\begin{cases}x=v_0 \cos\theta t \\ y=v_0 \sin\theta t-\frac{1}{2}gt^2 \\ \end{cases}$$

消去t，得到轨迹方程$$!y=x\tan\theta-\frac{gx^2}{2v_0^2}(1+\tan^2 \theta)$$

以$$\tan \theta$$为主元，化简得$$!\frac{gx^2}{2v_0^2}\tan^2 \theta -x\tan\theta+y+\frac{gx^2}{2v_0^2}=0$$

对任一点$$(x,y)$$，有

1、$$\tan \theta$$有两实根，能到达

2、$$\tan \theta$$无实根，不能到达

3、$$\tan \theta$$有单根，能到达的临界点

于是$$!\Delta=0\quad\Rightarrow\quad x^2=4\cdot\frac{gx^2}{2v_0^2}(y+\frac{gx^2}{2v_0^2})$$

$$!\Rightarrow\quad y=-\frac{g}{2v_0^2}x^2+\frac{v_0^2}{2g}$$

即为抛体运动的包络面。

我当时也知道好像是要化成关于$$\tan\theta$$的方程，但是不知道怎么化，有个$$\frac{1}{\cos^2\theta}$$。我太逗了，因为$$\sec^2\theta=1+\tan^2\theta$$

PS:其实即使到现在，我还是挺喜欢物理的。